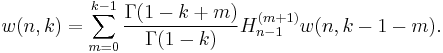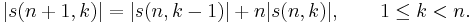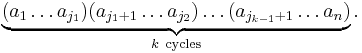Stirling numbers of the first kind
In mathematics, Stirling numbers of the first kind, together with the Stirling numbers of the second kind, are the two types of Stirling numbers. They commonly occur in combinatorics, where they appear in the study of permutations. The Stirling numbers of the first and second kind can be understood to be inverses of one-another, when taken as triangular matrices. This article is devoted to specifics of Stirling numbers of the first kind; further identities linking the two kinds, and general information, is given in the article on Stirling numbers.
Contents |
Definition
Unsigned Stirling numbers of the first kind
The unsigned Stirling numbers of the first kind count the number of permutations of n elements with k disjoint cycles.
The unsigned Stirling numbers arise as coefficients of the rising factorial, i.e.,
![(x)^{(n)} = x(x%2B1)\cdots(x%2Bn-1)=\sum_{k=0}^n \left[{n\atop k}\right] x^k](/2012-wikipedia_en_all_nopic_01_2012/I/07486e55ccd2bd9ab218d4f8750b8405.png) .
.
Most identities on this page deal with the unsigned Stirling numbers.
Stirling numbers of the first kind
Stirling numbers of the first kind (often without the qualifying adjective signed) are given by
They are the coefficients in the expansion
where 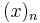 is the falling factorial
is the falling factorial
Note that
Warning: the notations for signed and unsigned Stirling numbers are sometimes defined just the other way round.
Recurrence relation and table of values for the unsigned Stirling numbers
The unsigned Stirling numbers of the first kind can be calculated by the recurrence relation
for 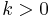 , with the initial conditions
, with the initial conditions
for n > 0.
The above follows from the recurrence relation on the rising factorials:
Below is a triangular array of unsigned values for the Stirling numbers of the first kind, similar in form to Pascal's triangle.
| n \ k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | |||||||||
| 1 | 0 | 1 | ||||||||
| 2 | 0 | 1 | 1 | |||||||
| 3 | 0 | 2 | 3 | 1 | ||||||
| 4 | 0 | 6 | 11 | 6 | 1 | |||||
| 5 | 0 | 24 | 50 | 35 | 10 | 1 | ||||
| 6 | 0 | 120 | 274 | 225 | 85 | 15 | 1 | |||
| 7 | 0 | 720 | 1764 | 1624 | 735 | 175 | 21 | 1 | ||
| 8 | 0 | 5040 | 13068 | 13132 | 6769 | 1960 | 322 | 28 | 1 | |
| 9 | 0 | 40320 | 109584 | 118124 | 67284 | 22449 | 4536 | 546 | 36 | 1 |
Simple identities
Note that although
and
Also
and
and
Similar relationships involving the Stirling numbers hold for the Bernoulli polynomials. Many relations for the Stirling numbers shadow similar relations on the binomial coefficients. The study of these 'shadow relationships' is termed umbral calculus and culminates in the theory of Sheffer sequences.
Combinatorial proofs
These identities may be derived by enumerating permutations directly. For example, how many permutations on [n] are there that consist of n − 3 cycles? There are three possibilities:
- n − 6 fixed points and three two-cycles
- n − 5 fixed points, a three-cycle and a two-cycle, and
- n − 4 fixed points and a four-cycle.
We enumerate the three types, as follows:
- choose the six elements that go into the two-cycles, decompose them into two-cycles and take into account that the order of the cycles is not important:
- choose the five elements that go into the three-cycle and the two-cycle, choose the elements of the three-cycle and take into account that three elements generate two three-cycles:
- choose the four elements of the four-cycle and take into account that four elements generate six four-cycles:
Sum the three contributions to obtain
Other relations
These include
where Hn is a harmonic number, and
where Hn(m) is a generalized harmonic number. A generalization of this relation to harmonic numbers is given in a later section.
And we have also:
where 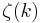 is the Riemann zeta function.
is the Riemann zeta function.
Generating function
A variety of identities may be derived by manipulating the generating function:
In particular, the order of summation may be exchanged, and derivatives taken, and then z or u may be fixed.
Similarly, we may derive:
Finite sums
A simple sum is
or in a more general relationship,
The identity
can be proved by the techniques on the page Stirling numbers and exponential generating functions.
Infinite sums
Some infinite sums include
where |z| < 1 (the singularity nearest to z = 0 of log(1 + z) is at z = −1.)
Explicit formula
The Stirling number s(n,n-p) can be found from the formula[1]
where
and
is a multinomial coefficient. The Kronecker delta in the first equation restricts the sums over the k's to a sum over the partitions of p.
Relation to harmonic numbers
Stirling numbers of the first kind can be expressed in terms of the harmonic numbers
as follows:
where w(n, 0) = 1 and
In the above, 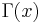 is the Gamma function.
is the Gamma function.
Enumerative interpretation
The absolute value of the Stirling number of the first kind, s(n, k), counts the number of permutations of n objects with exactly k orbits (equivalently, with exactly k cycles). For example, s(4, 2) = 11, corresponds to the fact that the symmetric group on 4 objects has 3 permutations of the form
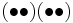 —2 orbits of size 2 each
—2 orbits of size 2 each
and 8 permutations of the form
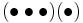 —1 orbit of size 3, and 1 orbit of size 1
—1 orbit of size 3, and 1 orbit of size 1
(see the entry on cycle notation for the meaning of the above expressions.)
Let us prove this. First, we can remark that the unsigned Stirling numbers of the first kind are characterized by the following recurrence relation:
To see why the above recurrence relation matches the count of permutations with k cycles, consider forming a permutation of n + 1 objects from a permutation of n objects by adding a distinguished object. There are exactly two ways in which this can be accomplished. We could do this by forming a singleton cycle, i.e. leaving the extra object alone. This accounts for the s(n, k − 1) term in the recurrence formula. We could also insert the new object into one of the existing cycles. Consider an arbitrary permutation of n objects with k cycles, and label the objects a1, ..., an, so that the permutation is represented by
To form a new permutation of n + 1 objects and k cycles one must insert the new object into this array. There are, evidently n ways to perform this insertion. This explains the n s(n, k) term of the recurrence relation. Q.E.D.
References
- The Art of Computer Programming
- Concrete Mathematics
- M. Abramowitz, I. Stegun, ed (1972). "§24.1.3. Stirling Numbers of the First Kind". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (9th ed.). New York: Dover. p. 824.
- Stirling numbers of the first kind, s(n,k) on PlanetMath.
- Sloane's A008275 : Triangle read by rows of Stirling numbers of first kind. The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
This article incorporates material from Stirling numbers of the first kind on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
![s(n,k) = (-1)^{n-k} \left[{n \atop k}\right] .](/2012-wikipedia_en_all_nopic_01_2012/I/7bed3ff9c7e76dd88360e6310b1c36fb.png)
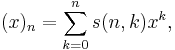
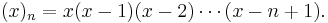
![\left[{n \atop k}\right] = \left|s(n,k)\right| .](/2012-wikipedia_en_all_nopic_01_2012/I/d0682a6784ade7f468c5d914fffc47f0.png)
![\left[{n%2B1\atop k}\right] = n \left[{n\atop k}\right] %2B \left[{n\atop k-1}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/e4ad85c8bf46166aeed9b71bf1c6cd46.png)
![\left[{0\atop 0}\right] = 1 \quad\mbox{and}\quad \left[{n\atop 0}\right]=\left[{0\atop n}\right]=0](/2012-wikipedia_en_all_nopic_01_2012/I/1b26c21495245a1d4992471523c5fcff.png)
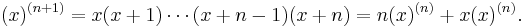
![\left[{0 \atop 0}\right] = 1\quad\mbox{we have}\quad\left[{n\atop 0}\right] = 0\quad \mbox{if} \quad n > 0](/2012-wikipedia_en_all_nopic_01_2012/I/f8a153ad75b506461e225756ccc5cc5d.png)
![\left[{0\atop k}\right] = 0\quad\mbox{if}\quad k > 0,\quad\mbox{or more generally,}\quad \left[{n\atop k}\right] = 0\quad\mbox{if}\quad k>n.](/2012-wikipedia_en_all_nopic_01_2012/I/98f86a5561c985ede0113a2c0293a29b.png)
![\left[{n \atop 1}\right] = (n-1)!](/2012-wikipedia_en_all_nopic_01_2012/I/3c9ed96d696b0dd66dda8b15c0fd9b4b.png)
![\left[{n\atop n}\right] = 1,
\quad
\left[{n\atop n-1}\right] = {n \choose 2},](/2012-wikipedia_en_all_nopic_01_2012/I/39716d4d774bf77f5449709dcea612f7.png)
![\left[{n\atop n-2}\right] = \frac{1}{4} (3n-1) {n \choose 3}\quad\mbox{ and }\quad\left[{n\atop n-3}\right] = {n \choose 2} {n \choose 4}.](/2012-wikipedia_en_all_nopic_01_2012/I/c1e72b52cc8bf7ab098710d3a8764302.png)
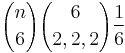
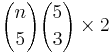
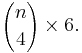
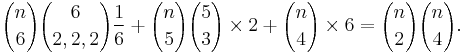
![\left[{n\atop 1}\right] = (n-1)!,](/2012-wikipedia_en_all_nopic_01_2012/I/8f6edf4ca1f5321e5daa4f800e5ec7d8.png)
![\left[{n\atop 2}\right] = (n-1)!\; H_{n-1},](/2012-wikipedia_en_all_nopic_01_2012/I/c2d57e73877d6e7cdaa91dacb52b0054.png)
![\left[{n\atop 3}\right] = \frac{1}{2} (n-1)! \left[ (H_{n-1})^2 - H_{n-1}^{(2)} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/0284e03fb7da7fe33957aff516ba9896.png)
![\left[{n\atop 4}\right] = \frac{1}{3!}(n-1)! \left[ (H_{n-1})^3 - 3H_{n-1}H_{n-1}^{(2)}%2B2H_{n-1}^{(3)} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/279cb9849388368e7ba85ccafc17e1b1.png)
![\sum_{n=i}^\infty \frac{\left[{n\atop i}\right]}{n (n!)} = \zeta(i%2B1)](/2012-wikipedia_en_all_nopic_01_2012/I/a717c5f22fb929a56d19990499853d7c.png)
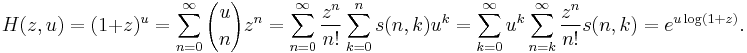
![G(z,u)= (1-z)^{-u}
= \sum_{k=0}^\infty u^k \sum_{n=k}^\infty \frac {z^n}{n!} \left[{n\atop k}\right] = e^{u\log(1/(1-z))}.](/2012-wikipedia_en_all_nopic_01_2012/I/677842dfbfc2f2b6e6abc181b2addaa7.png)
![\sum_{k=0}^n \left[{n\atop k}\right] = n!](/2012-wikipedia_en_all_nopic_01_2012/I/6a20be4b86fb9392f036fa3fa9186341.png)
![\sum_{k=0}^a \left[{n\atop k}\right] = n! - \sum_{k=0}^n \left[{n\atop k%2Ba%2B1}\right].](/2012-wikipedia_en_all_nopic_01_2012/I/42311adc0a9153a18ccd657b3c7c6cd8.png)
![\sum_{p=k}^{n} {\left[{n\atop p}\right]\binom{p}{k}} = \left[{n%2B1\atop k%2B1}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/f6c2a5d5eaf238aa43546cb86488be85.png)
![\sum_{n=k}^\infty (-1)^{n-k} \left[{n\atop k}\right] \frac{z^n}{n!} = \frac{\left(\log (1%2Bz)\right)^k}{k!}](/2012-wikipedia_en_all_nopic_01_2012/I/91fa47edc8715be43eb03499b69f1fe0.png)
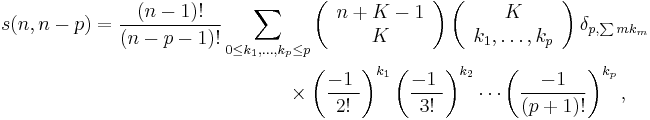
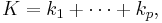
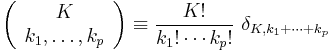
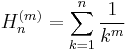
![\left[{n \atop k}\right]= \frac{\Gamma(n)}{\Gamma(k)}w(n,k-1)](/2012-wikipedia_en_all_nopic_01_2012/I/9a4805d35ffee7e7f6758fd62678c895.png)